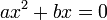¿Qué es una ecuación?
Es una expresión algebraica que consta de dos miembros separados por un signo de igualdad. Uno o ambos miembros de la ecuación debe tener al menos una variable o letra, llamada incógnita. Las ecuaciones se convierten en identidades sólo para determinados valores de la(s) incógnita(s). Estos valores particulares se llaman soluciones de la ecuación.
Ecuación: es una igualdad que tiene una o varias incógnitas, a su vez estas aceptan un valor o un grupo de valores.
PRIMER MIEMBRO >>>4 + 3x = x - 8 <<< SEGUNDO MIEMBRO
SIGNO IGUAL
Ejemplo:
La ecuación: 
3X - 8 = 10 sólo se cumple para X = 6, ya que si sustituimos dicho valor en la ecuación quedará la identidad: 10 = 10. Por lo tanto decimos que X = 6 es la solución de la ecuación dada. De hecho, es la única solución. Si usáramos, por ejemplo, X = 2, resultaría -2 = 10 (un absurdo) Resolver una ecuación es hallar los valores de X que la satisfacen a través de técnicas matemáticas variadas. Si la ecuación es de primer grado, un despeje es el procedimiento general. Si el grado de la ecuación es superior a uno, deben utilizarse otros métodos.
¿Qué es una ecuación cuadrática?
Es un tipo de ecuación particular en la cual la variable o incógnita está elevada al cuadrado, es decir, es de segundo grado. Un ejemplo sería: 2X2 - 3X = 9. En este tipo de ecuación no es posible despejar fácilmente la X, por lo tanto se requiere un procedimiento general para hallar las soluciones.
Una ecuación de segundo grado o ecuación cuadrática, es una ecuación polinómica donde el mayor exponente es igual a dos. Normalmente, la expresión se refiere al caso en que sólo aparece una incógnita y que se expresa en la forma:
donde a es el coeficiente cuadrático o de segundo grado y es siempre distinto del numero 0, b el coeficiente lineal o de primer grado y c es el término independiente.
CLASIFICACIÓN
La ecuación de segundo grado se clasifica de la siguiente manera:
1.- Completa: Tiene la forma:
donde los tres coeficientes a, b y c son distintos de cero.
2.- Incompleta pura: Es de la forma:
donde los valores de a y de c son distintos de cero. Se resuelve despejando x con operaciones inversas.
3.-Incompleta mixta: Es de la forma:
donde los valores de a y de b son distintos al numero cero. Se resuelve por factorización de x y siempre tiene la solución trivial x1 = 0.
MÉTODOS DE SOLUCIÓN
ECUACIÓN CUADRÁTICA COMPLETA:
X2 + X = 552 >>>>> ECUACIÓN
X2 + X - 552= 0 >>>>>> La pasamos a su forma general
( x + 24) ( x - 23) = 0 >>>>>>> Factorizamos
El primer término en ambos paréntesis corresponde a la raíz cuadrada del término cuadrático en la ecuación original (x ) ( x ), los segundos términos van a ser dos numeros que al sumar o restar nos den el coeficiente del termino lineal, en la ecuación original, y que a su vez al multiplicarlos nos den como resultado el término independiente ( +24) ( -23)
(x + 24)= 0 (x - 23 )= 0 >>>>>>> Se obtienen dos ecuaciones lineales.
Ambos factores ubicados en el primer miembro de la ecuación se igualan a cero
Se despeja a la incógnita en ambas ecuaciones, efectuando operaciones inversas.
x + 24 = 0 x - 23 = 0
x= 0 - 24 x = 0 + 23
x1= -24 x2= 23 se obtienen dos soluciones, es decir dos valores para x, uno + y otro -.
ECUACIONES CUADRÁTICAS INCOMPLETAS
PURAS
Dada la ecuación solo se despeja, es decir, se deja sola a la incógnita, efectuando operaciones inversas (contrarias).
Por ejemplo: 9x2= 64
1.- Se pasa a su forma general. 9x2 - 64 = 0
Nota: este paso solo es para identificar a que tipo de ecuación cuadrática corresponde.
2.- Se deja sola a la incógnita (despeja).
x2= 64/9 >>>>>> Como la división no da un numero exacto se deja indicada la operación.
x2 = √64/ 9 >>>>> y se saca raíz cuadrada por separado...
x1= +8/3 x2= -8/3
Dada la ecuación se factoriza... X2- 49= 0
Observa que en este caso es una DIFERENCIA DE CUADRADOS por lo que la factorización resulta:
(x +7 ) (x - 7) = 0
Se obtienen dos ecuaciones lineales:
(x +7 ) = 0 (x - 7) = 0
Se procede a despejar ambas ecuaciones lineales:
. x1= +7 x2= -7
Para factorizar una ecuación mixta es necesario obtener primero el monomio factor común (MFC), es decir, el máximo común divisor. Que consiste en tomar una vez los factores comunes con su exponente menor. Por ejemplo: 20 a2 + 15 a = 0
5a (4a + 3 )= 0
Donde: 5a es el MFC, posteriormente para obtener los términos que están dentro del paréntesis se dividen los términos de la ecuación original entre el MFC. 20 a2 / 5a = 4a y 15 a / 5a= 3a
EJERCICIO: 9x2 + 3x= 0
1.- Se factoriza por monomio factor común.
3x ( 3x + 1) = 0
2.- Se igualan a cero ambas expresiones lineales.
3x = 0 3x + 1 = 0
3.- se procede a despejar la incógnita.
x = 0 / -3 3x = -1
x = 0 x = -1/3
. x1= 0 x2= -1/3
De esta forma se obtienen dos soluciones y en este caso una de ellas es 0.
Métodos estándar
Estos métodos de solución se pueden aplicar a cualquier caso de ecuación cuadratica ya sea completa o incompleta.
Al igual que en los casos anteriores, este método consiste en dar valores a x, sustituirlos en la ecuación original y efectuar operaciones, para obtener el valor de "y", se tabulan, para así poder gráficar en un plano cartesiano y encontrar los valores de la incógnita que satisfacen la ecuación, ubicados sobre el eje de las "x". Al graficar obtenemos una parábola que marca las soluciones sobre el eje de las abscisas, comoo en el siguiente ejemplo.
Este gráfico indica que las soluciones de la ecuación seran 2 y -2.
Dada la formula ya establecida solo resta sustituir los valores de a, b y c, para efectuar operaciones, las soluciones serán dos una positiva y otra negativa, como en toda ecuación cuadratica.
